How to Perform a Wald Test in R | wald.test function in R

What is the Wald Test, a method used to test the significance of individual regression coefficients, and how can it transform your regression analysis in R?

Have you ever wondered how to assess the significance of specific predictors in your regression model or decide if a variable should remain in your analysis? The Wald Test in R offers a straightforward and efficient solution to these questions. It evaluates whether coefficients in a model are significantly different from zero, helping you test hypotheses and refine your models with precision.

Key points

• The Wald Test evaluates the significance of predictors in regression models by testing if coefficients differ from zero, aiding in model refinement and hypothesis testing.
• R provides efficient tools like the aod and sandwich packages, making it easy to perform the Wald Test, visualize results, and ensure robust statistical analysis.
• A real-world example using a medical dataset demonstrated how the Wald Test identifies significant predictors (e.g., treatment type) with clear code walkthroughs and interpretations.
• Compared to the Likelihood Ratio Test (LRT), the Wald Test is computationally efficient. However, alternatives like the Score Test or Bayesian approaches may be preferable in small datasets or complex scenarios.

Table of Contents

What is the Wald Test?

Wald Test is a statistical method used to evaluate the significance of parameters in a regression model. Specifically, it tests whether specific coefficients are significantly different from zero, which helps determine the relevance of predictors in explaining the dependent variable. By quantifying this relationship, the test clarifies whether to retain or exclude variables from your model that can affect the degrees of freedom.

For example, suppose you're analyzing car performance using the popular mtcars dataset in R. In that case, you can use the Wald Test to evaluate which factors (e.g., horsepower or weight) most significantly impact fuel efficiency. The Wald Test is widely used in economics, medicine, and social sciences, making it a versatile tool for data-driven research.

Why Use the Wald Test in R?

R is renowned for its powerful statistical capabilities, and it offers a variety of packages to streamline the process of performing a Wald test. Wald Test process. The AOD and sandwich packages allow for easy implementation and robust testing. Using the Wald Test in R is computationally efficient—it requires estimating a single model compared to other tests like the Likelihood Ratio Test (LRT).

R's open-source ecosystem also provides enhanced visualization and reporting tools, making it ideal for students and researchers aiming to improve their regression analyses. You can uncover insights with precision and efficiency by leveraging the Wald Test in R.

Understanding the Wald Test

At its core, the Wald Test evaluates whether specific predictors in your model contribute significantly to the outcome. It's especially useful in regression analysis when you need to assess the null hypothesis (H₀), which states that a coefficient equals zero, against the alternative hypothesis (H₁) that it does not.

For example:

• Null Hypothesis (H₀): Horsepower does not affect fuel efficiency.

• Alternative Hypothesis (H₁): Horsepower significantly impacts fuel efficiency.

If the Wald Test reveals that the coefficient for horsepower is statistically significant, you reject the null hypothesis, suggesting that horsepower is a meaningful predictor in your model. It is invaluable for refining models by focusing on relevant variables.

Statistical Basis

The Wald Test relies on a test statistic derived from the estimated coefficient and its standard error. Under the null hypothesis, this statistic follows a chi-squared distribution, enabling the calculation of p-values to determine significance.

Key assumptions:

1. Homoscedasticity: Equal variance of residuals across predictors.

2. Normality: Residuals follow a normal distribution.

Failing these assumptions may compromise test reliability. In such cases, you can apply robust standard errors using the sandwich package to improve accuracy. By meeting these assumptions, the Wald Test becomes a robust and reliable tool for hypothesis testing in regression models.

When to Use the Wald Test

The Wald Test often compares variables and identifies which predictors should remain in your model. If you’re analyzing the mtcars dataset to understand car performance, you can test whether weight or transmission type contributes more to the outcome.

Key questions to consider:

• Do all predictors significantly impact the dependent variable?

• Which variables can be safely removed without reducing model quality?

The Wald Test helps streamline your model by addressing these questions, ensuring only impactful predictors remain.

The Wald Test is particularly advantageous in scenarios requiring:

• Efficiency can be improved by ensuring that the model specifies relevant variables.: It is crucial to assess the efficiency of your model to the degrees of freedom. It requires estimating only one model, saving computational resources compared to tests like the LRT.

• Large Sample Sizes: Performs well with extensive data, providing reliable p-values for decision-making.

For example, researchers studying medical datasets can quickly test whether patient demographics influence health outcomes without repeatedly re-estimating models.

Before We start, Make sure you read the following:

• Comprehensive Guide: How to install RStudio
• How to Import and Install Packages in R: A Comprehensive Guide
• How to Import Data into R | Load Data file in R Programming
• Preprocess the data

Limitations of wald.test function

While the Wald Test is powerful, it’s not without limitations:

1. Small Sample Sizes: It may produce unreliable results as estimates become imprecise.

2. Coefficients Near Zero: Tests can be misleading when parameters are near zero, as standard errors tend to inflate.

To address these issues, consider alternative tests, such as the LRT or bootstrap methods, which offer greater accuracy in small datasets.

Setting Up for the Wald Test in R

Required Packages and Functions

To perform the Wald Test in R, ensure you have the following libraries installed:

• AOD: Provides the wald.test() function for hypothesis testing.

• Sandwich: Offers robust standard errors for improved accuracy.

• lmtest: Assists with model diagnostics and testing.

Install these packages using the command:

packages <- c("aod", "sandwich", "lmtest")
for (pkg in packages) {
  if (!require(pkg, character.only = TRUE)) {
    install.packages(pkg, dependencies = TRUE)
    library(pkg, character.only = TRUE)
  }
}

Preparing Your Dataset

Before running the test, ensure your data meets critical assumptions:

Assumptions!

1. Check Normality: Use the shapiro.test() function to evaluate residuals.

2. Linearity: Plot residuals against predictors to confirm a linear relationship.

Here’s how you can prepare the mtcars dataset:

data(mtcars)
summary(mtcars)
boxplot(mtcars[, c(1, 4, 6)],main = "Boxplot of mtcars Dataset", 
        xlab = "Variables", ylab = "Values",names = c("mpg", "hp", "wt"))

You create a foundation for applying the Wald Test by fitting a linear regression model.

Performing the Wald Test in R: Step-by-Step

Model Fitting

Start by creating a base regression model using the lm() function:

model <- lm(mpg ~ hp + wt, data = mtcars)
summary(model)

It predicts miles per gallon (mpg) based on horsepower (hp) and weight (wt).

Running the Test

Apply the wald.test() function to test coefficients:

wald.test(b = coef(model), Sigma = vcov(model), Terms = 2:3)

The output provides a chi-squared value and a p-value, indicating whether coefficients for horsepower and weight are significant.

Enhancing accuracy

If assumptions like homoscedasticity are violated, use robust standard errors:

robust_se <- vcovHC(model, type = "HC3")
wald.test(b = coef(model), Sigma = robust_se, Terms = 2:3)

It improves the reliability of your results, ensuring robust inferences.

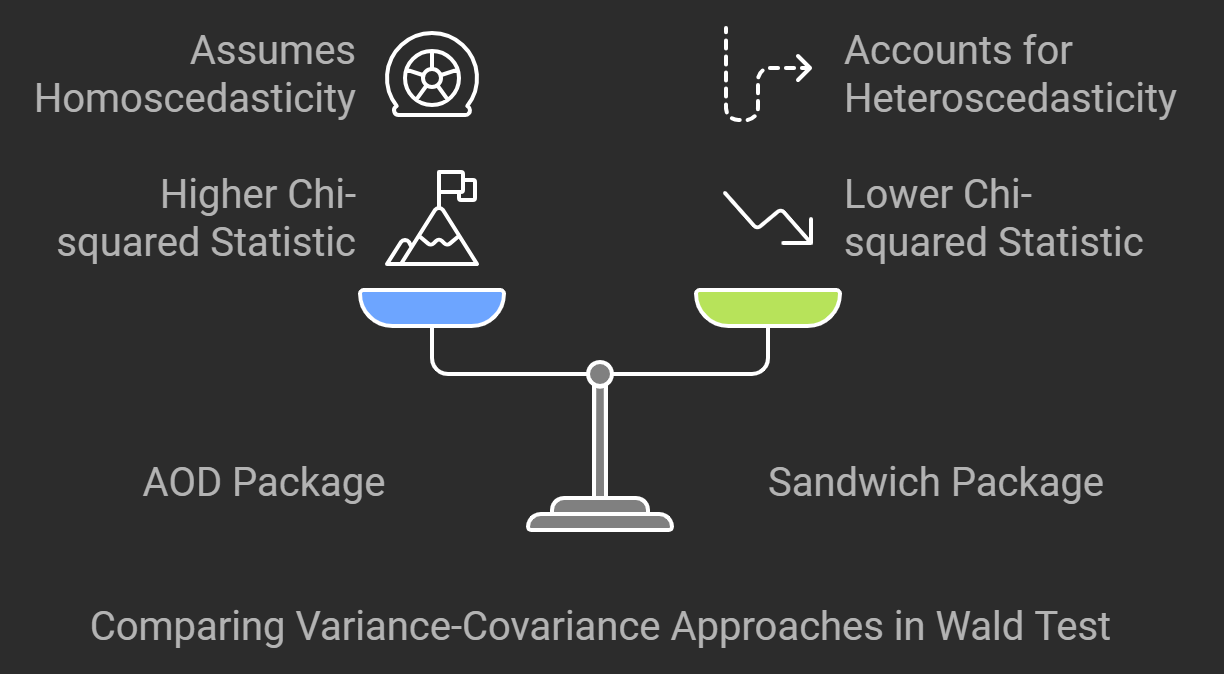
These two outputs differ in the variance-covariance matrix (Sigma) used for the Wald test. In the first test, the default variance-covariance matrix from the model (vcov(model)) assumes homoscedasticity (constant variance of errors). It leads to a higher Chi-squared statistic (138.4) and suggests more robust evidence against the null hypothesis. 

In the second test, a heteroscedasticity-consistent (HC3) variance-covariance matrix (vcovHC(model, type = "HC3")) is used, accounting for potential heteroscedasticity. This adjustment lowers the Chi-squared statistic (71.5), which reflects the model's consideration of error variance inconsistencies, but the result is still significant (P < 0.05). The robust method often gives more reliable inference under heteroscedasticity.

Practical Example of the Wald Test

Real-World Scenario: Assessing Predictors in a Medical Dataset

Imagine you're a researcher analyzing a medical dataset to predict patient recovery times based on various factors such as age, treatment type, and pre-existing conditions. The goal is to determine whether specific predictors, such as treatment type, significantly influence recovery.

Using the Wald Test, you can evaluate whether the coefficients for these predictors are statistically significant. It allows you to refine your model, ensuring that only meaningful variables are included in your analysis.

For instance, in the dataset:

• Dependent Variable: Recovery time in days.

• Predictors: Age, treatment type, and pre-existing conditions.

By applying the Wald Test in R, you can test hypotheses like:

• H₀ (Null Hypothesis): Treatment type does not affect recovery time (coefficient = 0).

• H₁ (Alternative Hypothesis): Treatment type significantly impacts recovery time (coefficient ≠ 0).

This real-world scenario highlights the test's practical use in hypothesis testing, providing actionable insights for medical decisions.

Walkthrough with Code

Let's walk through the application of the Wald Test using R.

People also read

Step 1: Load and Inspect the Dataset

Load a simulated medical dataset to ensure clarity.

set.seed(123)
medical_data <- data.frame(
  recovery_time = rnorm(100, mean = 10, sd = 3),
  age = rnorm(100, mean = 50, sd = 10),
  treatment = factor(sample(c("A", "B"), 100, replace = TRUE)),
  pre_existing = rbinom(100, 1, 0.3)
)
head(medical_data)

Step 2: Fit a Linear Model

Fit a regression model with lm():

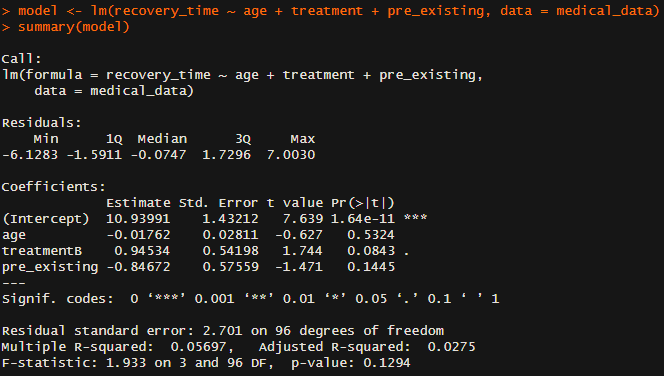
model <- lm(recovery_time ~ age + treatment + pre_existing, data = medical_data)
summary(model)

Step 3: Perform the Wald Test

Use the aod package for testing:

wald.test(b = coef(model), Sigma = vcov(model), Terms = 2:4)

Step 4: Interpret Results

The output includes a chi-squared value and p-value:

Chi-squared and P-value! If the p-value is below 0.05, reject H₀ and conclude that predictors significantly affect recovery time.

This practical example demonstrates the utility of the Wald Test in identifying influential predictors in real-world data.

Comparing the Wald Test with Other Tests

Wald Test vs Likelihood Ratio Test (LRT)

While the Wald and Likelihood Ratio Test (LRT) evaluates model parameters, their computational approaches and applications differ.

Feature	Wald Test	Likelihood Ratio Test
Computation	Single model estimation.	Requires two model estimations (full and reduced).
Efficiency	Faster, especially for large datasets.	Computationally intensive.
Assumptions	Sensitive to near-zero coefficients.	Robust with small sample sizes.
Output	Provides p-value via chi-squared statistic.	Compares likelihoods to compute significance.

When to Use Each

• Use the Wald Test for quick hypothesis testing with large datasets.

• Opt for the LRT when dealing with small samples or nested models for more excellent reliability.

Alternatives to Consider

1. Score Test: Suitable for initial hypothesis screening; relies on model gradients instead of parameter estimates.

2. Bootstrap Methods: Provide non-parametric confidence intervals, which are ideal for small datasets.

3. Bayesian Approaches: Offer posterior probabilities, which are helpful in cases requiring uncertainty quantification.

Selecting the correct test depends on sample size, computational resources, and specific analysis goals.

Tips for Interpreting Results

The Wald Test produces:

• Chi-Squared Value: Measures deviation of coefficients from zero.

• P-Value: Indicates statistical significance (e.g., p < 0.05 implies a rejection of H₀).

Example Interpretation

If the chi-squared value is high and the p-value is low, predictors like treatment type significantly impact recovery time in the medical dataset. Use these results to refine your model, retaining significant predictors for better accuracy.

Common Pitfalls

1. Overlooking Assumptions: Violations of normality or homoscedasticity can skew results. Always test assumptions with diagnostic plots.

2. Misinterpreting Coefficients: Statistical significance doesn't imply practical relevance. Check effect sizes to gauge real-world impact.

3. Relying Solely on P-Values: Combine p-value interpretation with confidence intervals to ensure robust conclusions.

Avoid these pitfalls to make informed decisions in your analysis.

Advanced Applications of the Wald Test

Generalized Linear Models (GLMs)

The Wald Test extends seamlessly to GLMs, including logistic and Poisson regressions. These models handle:

• Binary Outcomes: E.g., disease presence (yes/no).

• Count Data: E.g., number of hospital visits.

Example:

glm_model <- glm(recovery_time ~ age + treatment, family = poisson, data = medical_data)
wald.test(b = coef(glm_model), Sigma = vcov(glm_model), Terms = 2:3)

This flexibility makes the Wald Test invaluable for diverse data types.

Non-Linear Hypotheses

The Wald Test can also assess non-linear relationships by testing constraints on parameters. For example:

Hypothesis: Age has a quadratic effect on recovery time.

Testing these advanced hypotheses unlocks more profound insights into your models.

Visualizing Results for Better Understanding

Diagnostic Plots

Diagnostic plots help validate model assumptions and visualize test results:

• Residual Plots: Detect heteroscedasticity.

• Leverage Plots: Identify influential observations.

Example Code:

par(mfrow=c(1,2))
plot(model, which = 1:2)
dev.off()

These plots provide a quick health check for your model's validity.

Interpreting Graphs

Visualize regression model outputs with bar or scatter plots. Highlight significant predictors for straightforward interpretation.

Example:

library(ggplot2)
coef_plot <- data.frame(
  Coefficient = names(coef(model)),
  Estimate = coef(model))
ggplot(coef_plot, aes(x = Coefficient, y = Estimate)) +
  geom_bar(stat = "identity") +
  theme_minimal()}

Graphs make your findings more accessible, especially for presentations or reports.

The bar chart represents the estimated coefficients from a regression model. The y-axis shows the estimated values, while the x-axis lists the model predictors: an intercept, age, pre_existing (conditions), and treatmentB. The intercept has the most considerable magnitude, indicating a significant baseline effect. The coefficient for treatmentB is positive, suggesting it increases the dependent variable compared to the reference treatment. Conversely, pre_existing has a negative coefficient, implying a decreasing effect. The age coefficient is negligible or near zero, indicating it may not significantly impact the outcome. The chart suggests variable importance, with the intercept and treatmentB being the most notable.

Conclusion

The Wald Test is a cornerstone of regression analysis, providing a reliable and efficient method to evaluate the significance of predictors in statistical models. Its ability to test hypotheses about model coefficients helps researchers refine their models, ensuring only the most meaningful variables are retained. Whether you’re working with linear models, generalized linear models, or non-linear hypotheses, the Wald Test in R offers versatility and precision, making it an invaluable tool for students and researchers worldwide. Following the step-by-step guide outlined in this article, you can confidently apply the Wald Test to your datasets. Tools like the aod and sandwich packages simplify implementation while ensuring robust results. Visual aids, such as diagnostic plots, further enhance your ability to interpret and communicate findings effectively.

As you continue your data analysis journey, consider exploring advanced statistical techniques like the Likelihood Ratio Test, Score Test, or Bayesian methods. Each offers unique strengths that can complement the Wald Test, broadening your analytical toolkit and deepening your insights. With the foundational knowledge of the Wald Test, you’re now well-equipped to tackle complex data challenges and confidently make data-driven decisions. Dive deeper into R’s capabilities and unlock the full potential of statistical analysis.

Frequently Asked Questions (FAQs)

What does the Wald test do in R?

The Wald Test in R evaluates whether specific predictors in a regression model significantly contribute to the outcome variable. It tests the null hypothesis that the coefficients of predictors are equal to zero. By calculating the Wald statistic using the coefficient estimates and their standard errors, R determines if predictors are statistically significant. Tools like the aod package in R make implementing the Wald Test straightforward, aiding researchers in hypothesis testing and model refinement.

What is the Wald test?

The Wald Test is a statistical hypothesis test used to determine whether one or more coefficients in a regression model are significantly different from zero. It compares the estimated coefficients against a hypothesized value (typically zero) using a test statistic that follows a chi-squared distribution under the null hypothesis. It is commonly used in regression analyses to assess the relevance of variables.

What is the interpretation of the Wald test result?

The Wald Test result provides a test statistic and a p-value.

• Low p-value (e.g., < 0.05): Reject the null hypothesis, indicating the coefficient is statistically significant.
• High p-value (e.g., > 0.05): Fail to reject the null hypothesis, suggesting the coefficient may not significantly impact the model.
  This interpretation helps identify which predictors meaningfully contribute to the outcome.

What is the difference between the Z test and the Wald test?

The Z Test tests hypotheses about a population mean or proportion under the normality assumption, while the Wald Test evaluates regression coefficients. The Z test statistic is a special case of the Wald statistic when applied to single parameters. Wald Tests are commonly used in regression models, making them more flexible for testing multiple coefficients.

What is the use of Wald test in linear regression?

In linear regression, the Wald Test determines whether predictors are statistically significant. By testing the null hypothesis that a coefficient equals zero, it identifies whether a predictor has a meaningful impact on the dependent variable. This helps refine the model by retaining significant variables and discarding irrelevant ones, improving accuracy and interpretability.

What is the Wald test for heteroskedasticity?

The Wald Test for heteroskedasticity examines whether variance in residuals changes across levels of predictors. It tests if the null hypothesis of homoscedasticity holds. If rejected, it indicates heteroskedasticity is present, suggesting a need for robust standard errors or alternative models to address the issue.

How do you read a Wald test?

To read a Wald Test result:

• Look at the test statistic (e.g., chi-squared value).
• Check the p-value associated with the test statistic.
• P-value < 0.05: Reject the null hypothesis; the coefficient is significant.
• P-value > 0.05: Fail to reject the null hypothesis; the coefficient may not be significant.

Interpret these results in the context of your research question.

What is the p-value for the Wald test?

The p-value in the Wald Test quantifies the probability of observing the test statistic under the null hypothesis. A low p-value (typically < 0.05) indicates that the coefficient being tested is unlikely to equal zero, implying statistical significance. It’s a key metric to determine the relevance of predictors.

What is the importance of the Wald test variable?

The Wald Test variable is crucial for identifying significant predictors in a model. By testing if coefficients deviate significantly from zero, it helps in model optimization, ensuring only meaningful variables are included. This reduces noise and enhances the model's explanatory power and accuracy.

Is a Wald test an F-test?

No, the Wald Test and F-Test are different. The Wald Test uses a chi-squared statistic to evaluate individual or multiple coefficients. Conversely, the F-Test evaluates the overall significance of a regression model or compares nested models. Both serve distinct purposes in statistical analysis.

Is the Wald test a chi-square test?

Yes, the Wald Test is closely related to the chi-square test. Its test statistic follows a chi-squared distribution under the null hypothesis, especially when testing multiple coefficients simultaneously. This makes it a helpful tool for hypothesis testing in regression models.

What is the Wald test between the two models?

The Wald Test can compare nested models by testing the significance of additional predictors. Evaluating whether the added variables significantly improve model fit helps decide whether a simpler model is sufficient or if the extended model provides meaningful insights.

What is the significance of the Wald statistic?

The Wald statistic measures how far an estimated coefficient deviates from its hypothesized value (typically zero) relative to its standard error. A higher Wald statistic indicates more robust evidence against the null hypothesis, signaling the predictor’s significance in the model.

What is the purpose of the likelihood ratio test?

The Likelihood Ratio Test (LRT) compares the goodness-of-fit between two nested models—one simpler and one more complex. It evaluates whether the added complexity significantly improves the model’s explanatory power, often providing more reliable results than the Wald Test for small samples.

What is the difference between a T test and Wald test?

The T-Test evaluates the significance of a single parameter in linear regression using the t-distribution, typically for smaller sample sizes. The Wald Test uses a chi-squared distribution for single or multiple coefficients, making it more suitable for larger datasets and generalized regression models.

---

Transform your raw data into actionable insights. Let my expertise in R and advanced data analysis techniques unlock the power of your information. Get a personalized consultation and see how I can streamline your projects, saving you time and driving better decision-making. Contact me today at contact@rstudiodatalab.com or visit to schedule your discovery call.

Join Our Community Book a free call