The f-test in R is a powerful tool for comparing variances and drawing significant conclusions from your data. Understanding how to perform an F-test can transform your data analysis capabilities, allowing you to determine whether the variances in two samples are statistically different. In this comprehensive guide, we'll explore the f-test in R, from setting up your environment to interpreting the results. Whether you're a seasoned statistician or a data science newbie, mastering the test can elevate your analytical skills.
# Perform F-test to compare variances of mpg and hp
var1 <- mtcars$mpg
var2 <- mtcars$hp
var.test(var1, var2)Key Takeaways
- Understanding the F-Test: The f-test in R helps compare variances to determine if they are significantly different. It's crucial for statistical analysis and applications across various fields.
- Setting Up RStudio: Install and set up RStudio and load essential packages like Tidyverse and dplyr to streamline your data analysis process.install.packages("tidyverse")install.packages("dplyr")library(tidyverse)library(dplyr)
- Preparing and Testing Data: Import datasets, understand their structure, and check for normal distribution using the shapiro-wilk test with:data(mtcars)shapiro.test(mtcars$mpg)
- Performing and Interpreting F-Test: Conduct the f-test using the mtcars dataset to compare variances and interpret results based on p-value:
var.test(mtcars$mpg, mtcars$hp)
- Leveraging Resources and Communities: Enhance your skills by exploring tutorials, reading books by experts like Hadley Wickham, joining R programming communities, and using powerful R packages such as ggplot2 and dplyr.
Table of Contents
What is an F-Test?
An F-test is a statistical method used to determine if there are significant differences between the variances of two or more groups. The F-test compares the ratio of variances and is commonly applied in the context of ANOVA (Analysis of Variance) to test hypotheses about multiple group means. It helps understand whether the variability between group means is more significant than within the groups.
Pioneered by Ronald Fisher, the F-test has become a cornerstone in statistical analysis. Fisher's contributions laid the groundwork for modern statistical methods, and John Tukey further developed these concepts, enhancing their practical applications. These two statistical tests have made the F-test an essential tool for researchers.
Comparison Table: F-Test, T-Test, Shapiro-Wilk Test, and Z-Score
|
Aspect |
F-Test |
T-Test |
Shapiro-Wilk Test |
Z-Score |
|
Purpose |
Compares variances of two or more groups |
Compares means of two groups |
Tests for normality of a dataset |
Measures how many standard deviations a data point is from the mean |
|
Hypotheses |
H0: Variances are equal |
H0: Means are equal |
H0: Data is normally distributed |
No hypotheses, just a measure |
|
Formula |
(Variance of group 1) / (Variance of group 2) |
(Mean difference) / (Standard error of difference) |
Based on correlation between data and normal distribution |
(Data point - Mean) / Standard deviation |
|
Output |
F-statistic, p-value |
T-statistic, p-value |
W statistic, p-value |
Z-score |
|
Degrees of Freedom |
Num df (numerator), Denom df (denominator) |
df = n1 + n2 - 2 |
Depends on sample size |
Not applicable |
|
Used for |
Variance comparison |
Mean comparison |
Checking normality |
Standardization of data points |
|
Assumptions |
Samples are independent, normally distributed |
Samples are independent, normally distributed |
Data should be continuous and randomly sampled |
Data is normally distributed |
|
R Function |
var.test(x, y) |
t.test(x ~ y) |
shapiro.test(x) |
scale(x) |
|
Example R Code |
r var.test(mtcars$mpg, mtcars$hp) |
r t.test(mtcars$mpg ~ mtcars$cyl) |
r shapiro.test(mtcars$mpg) |
r z_scores <- scale(mtcars$mpg) |
Importance of Comparing Variances
Comparing variances, a fundamental statistical concept, is particularly relevant in quality control and finance.
-
In quality control, the F-test helps maintain consistent product quality by determining if observed differences in variances are due to random chance or a significant effect.
-
In finance, it aids in assessing the risk associated with different investment portfolios.
The F-test's robust method of comparing variances is vital in these scenarios, underlining its practical applications and relevance in these fields.
Overview of Variances
Variance, a measure of the spread of data points around the mean, is a critical concept in statistical analysis. It indicates the degree of variability within a dataset. The variance calculation involves adding the squared differences between each data point and the mean, then dividing by the number of observations. And understanding the two primary types of variances-
-
Population variances
Sample variances
Population variances measure the spread of all data points in an entire population. It quantifies how much individual data points differ from the population mean. This type of variance is crucial when the population as a whole is accessible, and data can be collected from every member. It provides a complete picture of variability within the population. The formula for population variance involves summing the squared differences between each data point and the population mean and then dividing by the total number of data points.
Sample variances estimate the variability within a sample drawn from a larger population. This measure is essential when studying the entire population is impractical or impossible. The formula for sample variance is similar to that of population variance. Still, it divides the sum of squared differences by the number of observations minus one (n-1) to account for the degrees of freedom. This adjustment corrects the bias in estimating the population variance from a sample.
Comparison Table: Population Variances vs. Sample Variances
|
Aspect |
Population Variances |
Sample Variances |
|
Definition |
Variance calculated using the entire population |
Variance estimated from a sample of the population |
|
Formula |
The sum of squared differences / N |
The sum of squared differences / (n-1) |
|
Use Case |
When entire population data is available |
When only a subset of the population is available |
|
Bias Adjustment |
No adjustment needed |
Adjusted by dividing by (n-1) |
|
Representativeness |
A complete picture of population variability |
Estimation of population variability |
|
Example Calculation |
Sum((X_i - μ)^2) / N |
Sum((X_i - x̄)^2) / (n-1) |
Performing F-Test in R
Data analysts or researchers must understand how to perform an F-test in R. The f-test allows us to compare the variances of two or more samples, providing insights into the consistency and variability of datasets. By leveraging the mtcars dataset, we can apply theoretical knowledge to real-world data, enhancing our analytical capabilities.
Getting Started with R Programming
To start with R programming, the first step is to install and set up RStudio, an integrated development environment (IDE) for R. RStudio, with its user-friendly interface, provides a comfortable environment to write, test, and debug R code, making the learning process smoother for data analysts and researchers.
install.packages("tidyverse")
install.packages("dplyr")
library(tidyverse)
library(dplyr)Preparing Your Data
Once RStudio is set up and the necessary packages are loaded, the next step is to import your dataset into R. For this tutorial, we will use the mtcars dataset, which is readily available in R. This dataset is often used in statistical analysis and contains various attributes of cars, such as miles per gallon (mpg), horsepower (hp), and more. Understanding the mtcars dataset is crucial for performing accurate analyses.
# Load the mtcars dataset data(mtcars) head(mtcars)
Before conducting an F-test, checking if the data is normally distributed is important, as the F-test assumes normality. The Shapiro-Wilk test is commonly used to check this assumption.
# Perform Shapiro-Wilk test for normality shapiro.test(mtcars$mpg) shapiro.test(mtcars$hp)
The Shapiro-Wilk test, a powerful tool in statistical analysis, assesses the normality of the mtcars dataset's mpg and hp variables. For mpg, the test statistic (W = 0.94756) and p-value = 0.1229 indicate that the data is not significantly different from a normal distribution, suggesting normality. This result implies that the mpg variable can be normally distributed, which is crucial for many statistical tests. However, for hp, the test statistic (W = 0.93342) and p-value = 0.04881 are just below the 0.05 threshold, indicating a slight deviation from normality.
If Normality Assumptions are violated
You can apply a data transformation to address the violation of normality assumptions for hp in the mtcars dataset. Common transformations include logarithmic, square root, or Box-Cox transformation, which can help normalize the data.
# Logarithmic transformation mtcars$log_hp <- log(mtcars$hp) # Re-test for normality shapiro.test(mtcars$log_hp)
This process involves creating a new variable, log_hp, by applying the log transformation to hp. Then, re-run the Shapiro-Wilk test on the transformed data to check for improved normality. If the p-value increases above 0.05, the normality assumption is likely satisfied.
The Shapiro-Wilk test results for log_hp (W = 0.97026, p-value = 0.5065) indicate that the data is not significantly different from a normal distribution. The high p-value suggests the normality assumption is satisfied after the logarithmic transformation.
Writing the F-Test Script
Now that the data is prepared and the normality assumption is checked, we can write the script to perform an F-test. It involves computing the ratio of variances between two samples and interpreting the results.
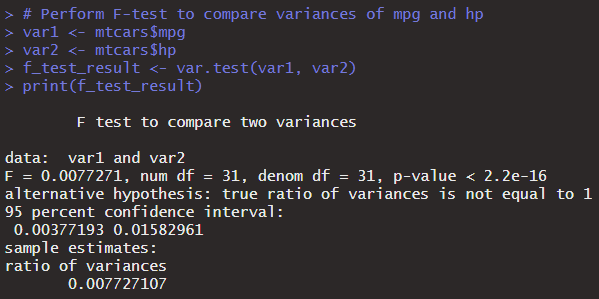
# Perform F-test to compare variances of mpg and hp var1 <- mtcars$mpg var2 <- mtcars$hp f_test_result <- var.test(var1, var2) print(f_test_result)
In the code snippet above, we first extract the variables of interest (mpg and hp) from the mtcars dataset. We then use the var.test() function to perform the f-test, which compares the variances of these two variables. The result provides the F-statistic and the p-value. The F-statistic measures the ratio of the variances, and the p-value indicates the probability of observing the data given that the null hypothesis is true. A low p-value suggests that the variances are significantly different.
The F-test results indicate a significant difference between the variances of var1 and var2. The F-statistic is 0.0077271, with degrees of freedom (df) for the numerator and denominator at 31. The extremely low p-value (< 2.2e-16) strongly rejects the null hypothesis that the variances are equal, supporting the alternative hypothesis that the true ratio of variances is not equal to 1. The 95% confidence interval for the ratio of variances is [0.00377193, 0.01582961], and the sample estimate for the ratio of variances is 0.007727107, indicating significantly different variances.
Using the F-Test to Compare Two Variances
The F-test is a crucial tool in statistical analysis, particularly when comparing the variances of two samples. It helps determine whether the variances from two different populations are equal. By applying the f-test in R, we can make informed decisions based on data variability. Formulating hypotheses, setting significance levels, and interpreting results are essential for accurate analysis.
Hypothesis Testing with F-Test
In hypothesis testing, we start by formulating the null and alternative hypotheses. For an F-test, the null hypothesis typically states that the variances of the two samples are equal. In contrast, the alternative hypothesis suggests that the variances are not equal.
|
Aspect |
Null Hypothesis (H0) |
Alternative Hypothesis (H1) |
|
Definition |
Assumes no effect or no difference |
Suggests there is an effect or a difference |
|
Notation |
H0 |
H1 |
|
Purpose |
Acts as a starting point for statistical testing |
Proposes an alternative to be tested against H0 |
|
Assumption |
Assumes equality or no relationship |
Indicates inequality or a relationship |
|
Example Statement |
Variances of mpg and hp are equal |
Variances of mpg and hp are not equal |
|
Basis of Test |
Tested directly through statistical methods |
Accepted only if H0 is rejected |
|
Decision Rule |
Fail to reject H0 if evidence is insufficient |
Reject H0 in favor of H1 if evidence is strong |
|
Significance Level |
Compared against the p-value to make a decision |
Determined by the p-value relative to the significance level |
|
Type of Error |
Risk of Type I error (false positive) if H0 is wrongly rejected |
Risk of Type II error (false negative) if H1 is wrongly not accepted |
|
Hypothesis Testing |
Maintains the status quo |
Suggests a change or difference |
Setting the significance level (commonly denoted as α) is the next step, usually at 0.05. This significance level helps determine the threshold for rejecting the null hypothesis. The p-value obtained from the f-test indicates the probability of observing the test results under the null hypothesis. We reject the null hypothesis if the p-value is less than the significance level.
# Formulating hypotheses and setting the significance level # H0: Variances of mpg and hp are equal # H1: Variances of mpg and hp are not equal significance_level <- 0.05 # Perform F-test f_test_result <- var.test(mtcars$mpg, mtcars$hp) print(f_test_result)
Interpreting F-Test Results
Interpreting the results of an f-test involves analyzing the f-statistic and the p-value. Suppose the p-value is less than the significance level (e.g., 0.05). In that case, it indicates that the variances are significantly different, leading to rejecting the null hypothesis. Visualization tools like the q-q plot can help understand the data distribution. Additionally, levene's test can be used as an alternative to check the equality of variances, which is less sensitive to non-normal distributions.
# Analyzing F-test results and visualizing with q-q plot
if (f_test_result$p.value < significance_level) {
print("Reject the null hypothesis: The variances are significantly different.")
} else {
print("Fail to reject the null hypothesis: The variances are not significantly different.")
}
par(mfrow=c(1,2))
# Visualizing with q-q plot
qqnorm(mtcars$mpg, main="Q-Q Plot for mpg")
qqline(mtcars$mpg)
qqnorm(mtcars$hp, main="Q-Q Plot for hp")
qqline(mtcars$hp)By following these steps, researchers and analysts can effectively use the f-test in R to compare variances, making well-informed decisions based on statistical evidence. This method not only enhances the reliability of the analysis but also ensures that the results are grounded in robust statistical principles.
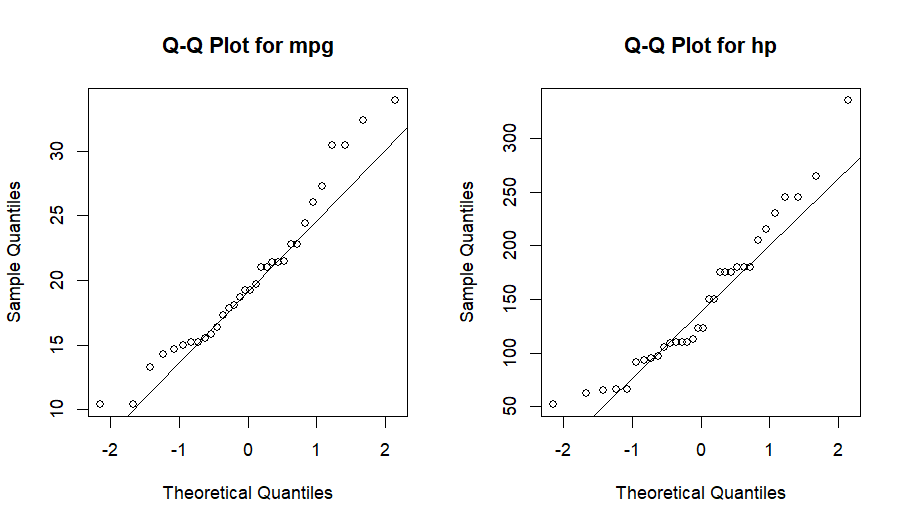
The Q-Q plots display the normality of the mpg and hp variables from the mtcars dataset. The Q-Q plot for mpg (left) shows data points closely aligned with the diagonal line, indicating that mpg reasonably follows a normal distribution. However, there are slight deviations at the tails.
Conversely, the Q-Q plot for hp (right) exhibits noticeable deviations from the diagonal line, especially at the higher values, suggesting that hp deviates from a normal distribution. These visual assessments support the Shapiro-Wilk test results, confirming mpg is normally distributed while hp is not.
Practical Applications of F-Test in Data Science
The F-test, a versatile tool in data science, is not just a theoretical concept but a practical solution that aids decision-making and significantly improves data insights. Its applications extend beyond theoretical analysis to practical, real-world scenarios, making it a valuable asset for any data scientist.
- How to min max scaling in r
- How to perform Repeated Measures ANCOVA in R
- How to calculate Confidence Interval in R
Case Study: Comparing Measurement Methods
In a practical application of the F-test, we conduct a case study comparing a new measurement method to an old one using the mtcars dataset. The aim is to determine if the variability of the new measurement is significantly different from the old method, thereby assessing the reliability and precision of the new method.
Real-World Example: Suppose a car manufacturer wants to compare the fuel efficiency measurement methods. Using the mtcars dataset, we can compare the variance in miles per gallon (mpg) recorded by the old and new methods.
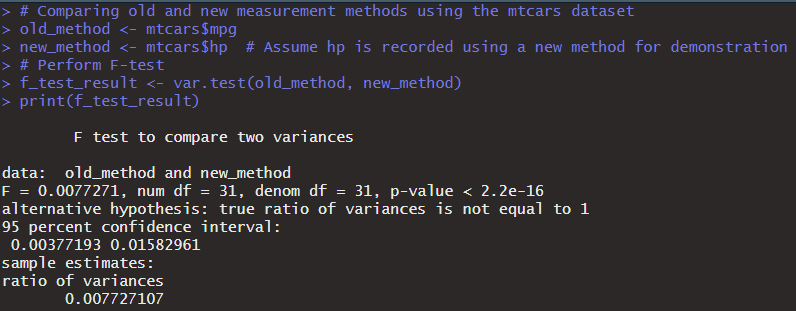
# Comparing old and new measurement methods using the mtcars dataset
old_method <- mtcars$mpg
new_method <- mtcars$hp # Assume hp is recorded using a new method for demonstration
# Perform F-test
f_test_result <- var.test(old_method, new_method)
print(f_test_result)Advanced Techniques with F-Test
Advanced techniques, such as the s3 method and fligner-killeen test, further enhance the application of the F-test. The s3 method enables complex object-oriented programming in R. At the same time, the fligner-killeen test is a valuable tool for comparing variances in non-normally distributed data, expanding the scope of the F-test in data analysis.
To handle complex datasets, we might take a random sample of 10 rows from the mtcars dataset to perform these tests.
# Advanced techniques using s3 method and fligner-killeen test set.seed(123) sample_data <- mtcars[sample(1:nrow(mtcars), 10), ] # Fligner-Killeen test for homogeneity of variances fligner_test_result <- fligner.test(sample_data$mpg ~ sample_data$cyl) print(fligner_test_result)
F-Test in Machine Learning
In machine learning, the F-test is a tool and a crucial element in model validation. It plays a significant role in comparing the variances of errors from different models, ensuring the chosen model is accurate and consistent. By leveraging the F-test, we can enhance model accuracy and reliability, making it an indispensable tool for any machine learning practitioner.
Enhancing Model Accuracy: Suppose we validate a regression model's performance on the mtcars dataset. We can determine which model performs better by comparing the variances of residuals (errors) from two different models.
# F-test in machine learning for model validation model1 <- lm(mpg ~ wt + hp, data = mtcars) model2 <- lm(mpg ~ wt + hp + qsec, data = mtcars) # Extract residuals residuals1 <- residuals(model1) residuals2 <- residuals(model2) # Perform F-test to compare variances of residuals f_test_residuals <- var.test(residuals1, residuals2) print(f_test_residuals)
The F-test results for comparing the variances of residuals from two regression models indicate that the ratio of variances (F = 1.0483) is close to 1, with a p-value of 0.8963. This high p-value suggests no significant difference exists between the variances of the residuals of the two models. The 95% confidence interval (0.5117245 to 2.1475483) includes 1, indicating that the variances are similar. Thus, adding **qsec** as a predictor in model 2 does not significantly affect the variance of the residuals compared to model 1. Both models perform similarly in terms of residual variance.
Additional Resources and Further Reading
Exploring additional resources is essential to deepen your understanding of the F-test in R and enhance your data analysis skills. These resources include tutorials, courses, community support, and powerful tools and libraries to aid your learning journey.
Recommended Tutorials and Courses
Several top online tutorials and courses are available to help you understand the F-test in R. Websites like Coursera, DataCamp, and Udemy offer courses that cover the F-test and other statistical tests. These courses provide step-by-step instructions, practical examples, and interactive exercises.
Books and Publications: To gain deeper insights, consider reading books by renowned experts like Hadley Wickham. His books, such as "R for Data Science" and "Advanced R," offer extensive knowledge of R programming, data manipulation, and statistical analysis. These publications are invaluable for both beginners and advanced users.
Community and Support
Joining R programming communities and forums can significantly enhance your learning experience. Platforms like Stack Overflow, RStudio Community, and Reddit's r/Rlanguage provide spaces to ask questions, share knowledge, and collaborate with other R users. Engaging with these communities can help you solve problems faster and gain new perspectives on your work.
Following Influential Data Scientists: To stay updated with the latest trends and techniques in data science, follow influential data scientists on social media platforms like Twitter and LinkedIn. Experts such as Hadley Wickham, Jenny Bryan, and David Robinson frequently share valuable insights, tutorials, and resources.
Tools and Libraries
Several essential packages can enhance your workflow for practical statistical analysis in R. ggplot2 is a powerful package for data visualization, allowing you to create complex plots easily. dplyr is another crucial package for data manipulation, providing a set of functions to work efficiently with data frames. Bioconductor is a repository of R packages for bioinformatics, offering tools for analyzing genomic data.
Using CRAN and Other Repositories: The Comprehensive R Archive Network (CRAN) is a vast repository of R packages. It provides access to a wide range of tools for statistical analysis, data visualization, and more. Additionally, GitHub is a valuable resource for finding the latest R packages and projects the community shares.
Common Errors and Fixes When Performing Statistical Tests in R
When working with R for statistical tests like the f-test, t-test, Shapiro-Wilk test, and calculating z-scores, beginners may encounter several common errors. Here are some of these errors and their solutions:
Error: "Object not found"
This error occurs when the object or variable name you are trying to use does not exist in your environment. Ensure the dataset and variable names are correctly spelled and loaded into the environment.
Solution: Check if the dataset is loaded and variable names are spelled correctly.
# Load the dataset data(mtcars) # Correctly spell variable names mpg_data <- mtcars$mpg
Error: "non-numeric argument to binary operator"
This error happens when the function expects numeric data but receives non-numeric data. For example, if you're trying to calculate the mean of a character variable, you'll get this error. Ensure the variables used in the tests are numeric.
Solution: Convert the variables to numeric if they are not.
# Convert to numeric if necessary mtcars$mpg <- as.numeric(mtcars$mpg)
Error: "data are essentially constant"
This error appears during the Shapiro-Wilk test when the data lacks variability, i.e., all values are nearly the same.
Solution: Check the data for variability and ensure a range of values.{
# Check for variability summary(mtcars$mpg)
Error: "not enough 'x' observations."
This error occurs when there are insufficient data points to perform the statistical test, such as in the Shapiro-Wilk test. It's a common error many beginners encounter, so don't worry if you encounter it.
Solution: Ensure your dataset has enough observations (usually more than 3 for the Shapiro-Wilk test).
# Ensure sufficient data points
if(length(mtcars$mpg) > 3) {
shapiro.test(mtcars$mpg)
} else {
print("Not enough observations for Shapiro-Wilk test")
}Error: "fewer than two groups"
This error occurs in t-test or f-test when there are only two groups to compare.
Solution: Verify that the grouping variable has at least two groups.
# Ensure there are at least two groups
table(mtcars$cyl)Error: "NaNs produced"
This error indicates that there are non-numeric or infinite values in the dataset, which cause the function to fail.
Solution: Remove or handle NaNs and infinite values before performing tests.
# Remove NaN and infinite values
clean_data <- na.omit(mtcars$mpg)
clean_data <- clean_data[is.finite(clean_data)]Error: "subscript out of bounds"
This error occurs when attempting to access an element outside the range of the dataset indices.
Solution: Ensure that the indices used are within the bounds of the dataset.
# Check the length of the dataset
length(mtcars$mpg)
# Access elements within the range
mtcars$mpg[1:10]By understanding and addressing these common errors, beginners can ensure a smoother experience when performing statistical tests in R. This proactive approach will help maintain the integrity of your data analysis and improve the accuracy of your results.
Conclusion
Mastering the f-test in R opens up a world of possibilities in data analysis and empowers you to compare variances and draw meaningful conclusions from your data. This skill is a theoretical and practical tool that can significantly enhance your data analysis capabilities. We've explored the definition and significance of the f-test, delving into its historical background with contributions from giants like Ronald Fisher and John Tukey. Understanding the importance of comparing variances is crucial, as it plays a vital role in fields ranging from quality control to finance. We detailed the calculation of variances, distinguishing between population and sample variances and providing clear examples with the mtcars dataset.
In practical applications, we demonstrated how to compare measurement methods, assess the variability of new measurements, and use advanced techniques such as the s3 method and the fligner-killeen test. But the real excitement lies in the role of the f-test in machine learning. It's not just a tool for model validation but a key player in enhancing accuracy and unlocking the full potential of your models. We recommended top tutorials and books by experts like Hadley Wickham to support your continued learning. We emphasized the value of joining R programming communities and following influential data scientists. Essential tools and libraries like ggplot2, dplyr, and Bioconductor were also discussed, along with the importance of utilizing repositories like CRAN.
Integrating these insights and resources can elevate your data analysis skills and make more informed decisions. But it doesn't stop there. The journey of mastering data science is ongoing, and each step you take builds a stronger foundation for your analytical capabilities. Keep learning, stay curious, and embrace the power of the F-test in your data analysis endeavors. Remember, the more you learn, the more you can achieve in data analysis.
Frequently Asked Questions (FAQs)
How do I compute the f-test in R?
What is the transcript of an F-test?
The transcript of an f-test typically includes the F-statistic, degrees of freedom (df), and the p-value, which helps determine if the variances are significantly different.
How do you perform an f-test to compare two samples?
What is a test to compare two variances?
A test to compare two variances is known as the f-test. It evaluates whether the variances of the two samples are significantly different.
What is the difference between the f-test and the t-test?
How are variances in R calculated?
What are statistical methods for variance comparison?
Statistical methods for variance comparison include the F-test and Levene's test. The f-test is used to compare two variances.
How do method 1 and method 2 differ in variance comparison?
Method 1 might refer to using an f-test, while method 2 could involve using Levene's test for variance comparison.
How to perform a default f-test to compare variances in R?
How do you specify parameters for an f-test in R?
What is the true ratio of variances?
The true ratio of variances is the actual ratio between two population variances. An F-test helps estimate if this ratio is significantly different from a confidence level equal to 1 95 percent.
When is the f-test used?
The f-test compares two variances, particularly in ANOVA tests or when checking model assumptions in regression analysis.
How do you compare two variances of data?
How to subscribe for updates on statistical methods?
To stay updated, you can subscribe to newsletters or blogs related to R and statistical methods, such as those offered by RStudio or DataCamp.
What are the steps to compute the f-test in R?
How do you perform a two-sample t-test?
What are num df and denom df in f-test?
Num df (numerator degrees of freedom) and denom df (denominator degrees of freedom) are terms used in the f-test to describe the degrees of freedom associated with the variances being compared.
How do we perform a two-sample t-test to check the equality of variances?
How do we assess the variability of a new measurement method?
What is a transcript in the context of statistical tests?
In statistical tests, a transcript includes the detailed output, such as the F-statistic, p-value, and degrees of freedom from an f-test.
When to use f-tests in statistical analysis?
F-tests are used when comparing variances or as part of ANOVA to determine if group means differ significantly by examining the variance within groups.
What should you do if you want to perform a two-variance test?
How can a t-test be used to check the equality of the variances?
What if you want to compare the variability of two samples?
How is an F-test used to test whether variances are equal?
What are the options for the alternative hypothesis in an F-test?
How do you determine if a new method reduces variability?
What are method 1 and method 2 for comparing variances?
Method 1 might refer to the f-test, and method 2 could be Levene's test for comparing variances.
How to check the normality of a variable in R?
What does an F-test in R tell you?
An F-test in R, a powerful tool, compares the variances of two or more groups to determine if they are significantly different. This test is theoretical and practical, crucial in comparing measurement methods, ensuring data reliability across samples, and validating statistical models. Its application in real-world scenarios makes it a must-know for statisticians, data analysts, and researchers.
What is the difference between the F-test and the t-test in R?
The primary difference between an F-test and a t-test in R lies in their purposes. An F-test compares the variances of two or more groups, whereas a t-test compares the means of two groups. The F-test helps in understanding the spread or variability within the data. At the same time, the t-test assesses whether the group means are significantly different.
What is the F-test in a regression model?
The F-test evaluates whether the overall regression model is significant in a regression model. It tests if at least one of the predictors is significantly related to the response variable. This helps determine the model's goodness-of-fit, indicating whether the predictors have a meaningful relationship with the outcome.
How do I do an F-test?
How do we interpret F-test results?
To interpret F-test results, look at the F-statistic and the p-value. Suppose the p-value is less than the significance level (commonly 0.05). In that case, it indicates that the variances are significantly different, leading to rejecting the null hypothesis. The F-statistic indicates the ratio of variances; a higher value suggests more significant variance differences.
What F value is significant?
An F value is considered significant if the associated p-value is less than the chosen significance level (typically 0.05). It indicates that the variances between the groups are significantly different.
Why do we use the F-test?
We use the F-test to compare variances between groups, assess model significance in regression, and validate the assumptions of other statistical tests. It helps determine if observed differences in variability are statistically significant.
What is the p-value of the F-test?
The p-value of the F-test indicates the probability of observing the data if the null hypothesis is true. A low p-value (typically < 0.05) suggests that the variances are significantly different, leading to rejecting the null hypothesis.
What is the purpose of the t-test in R?
The purpose of the t-test in R is to compare the means of two groups to determine if they are significantly different. It helps assess whether the observed differences between groups are due to random chance or a true effect.
Which regression technique uses the F-test or t-test?
Multiple regression techniques, such as linear regression and ANOVA, use the F-test and t-test. The F-test evaluates the overall model significance, while the t-test assesses the significance of individual predictors.
What is the F-test and its assumptions?
The F-test, a powerful statistical tool, compares variances. However, it's important to note that it assumes the samples are independent, normally distributed, and come from populations with equal variances. These assumptions are not just technicalities but crucial for the validity of the test results. Understanding and respecting these assumptions is key to ensuring the accuracy and reliability of your data analysis.
What does the t-test tell you?
The t-test tells you whether the means of the two groups are significantly different from each other. It evaluates the difference in means relative to the variability in the data, helping determine if the observed differences are statistically significant.
When to use F-test vs t-test?
Use an F-test when you need to compare variances between groups or assess the overall significance of a regression model. A t-test is used when comparing the means of two groups to determine if they are significantly different.
Is F-test and ANOVA the same?
The F-test and ANOVA are related but not the same. ANOVA uses the F-test to compare the variances among group means and determine if they have significant differences.
What if the F-statistic is less than 1?
If the F-statistic is less than 1, it indicates that the variance of the first group is less than the variance of the second group. It may still lead to significant results if the p-value is low.
How do we interpret the F-statistic in regression in R?
To interpret the F-statistic in regression, check the p-value associated with it. A low p-value (typically < 0.05) indicates that the regression model is significant, suggesting that at least one predictor variable significantly affects the response variable.
What is an F-test in regression?
An F-test in regression evaluates the overall significance of the regression model. It tests whether the explained variance in the response variable by the predictors is significantly greater than the unexplained variance.
What does an F-test of 1 mean?
An F-test of 1 means that the variances of the two groups are equal. In this case, the variance between groups equals the variance within groups.
How to use F-test?
What is considered a large F value?
A large F value indicates a significant difference between group variances. The exact threshold for "large" depends on the degrees of freedom and the analysis context. Still, a larger F value corresponds to a lower p-value and greater significance.
How to report F-statistics?
To report the F-statistic, include the F value, degrees of freedom for the numerator and denominator, and the p-value. For example: "F(1, 30) = 5.43, p < 0.05."
What is an F in a test?
In the context of statistical tests, F refers to the F-statistic, a ratio of variances used in the F-test to compare the variability between groups or within a regression model.
What does a partial F-test tell you?
A partial F-test assesses the significance of a subset of predictors in a regression model, determining if the additional predictors significantly improve the model compared to a simpler model.
What is the difference between ANOVA and F-test?
ANOVA (Analysis of Variance) uses the F-test to compare the means of three or more groups. The F-test is a broader term for comparing variances or testing overall model significance in regression.
What is the F-test for comparing two variances?
The F-test for comparing two variances determines if there is a significant difference between the variances of two samples. It is commonly used to test assumptions of equal variances in statistical models.
Does f mean fail?
In a statistical context, F does not mean fail. It refers to the F-statistic used in the F-test.
What does F stand for in results?
In statistical results, F stands for the F-statistic, a measure used to compare variances or assess the overall significance of a regression model.
What is the 5-point grading scale?
The 5-point grading scale evaluates performance, typically using grades A, B, C, D, and F, where A is excellent, B is good, C is average, D is below average, and F indicates fail.
Do you need help with a data analysis project? Let me assist you! With a PhD and ten years of experience, I specialize in solving data analysis challenges using R and other advanced tools. Reach out to me for personalized solutions tailored to your needs.
" " "